Spoliers Don’t read any of this if you want to try and solve Tuva or Bust! Tuva or Bust started as an idea purposed by Rob for a shell/sub-meta for the Feynman Round:
You get a page full of unlabeled bubbles connected by unlabeled arrows (with a small box in them where a one-letter label could go). The arrows form a tree pointing inward to the single labeled bubble, “Tannu Tuva”. You also get a bank of 26 possible relations between current and historical countries of the 20th century, such as “has a land border with”, “gained independence from”, “occupied by”, “fought a war against”, “disputes territory with”, “has the same head of state as”… The labels fall into rows that can be filled by the puzzle answers. The goal is to figure out the only possible mapping from relations to letters, and therefore to figure out the set of starting points (leaf nodes) that get you to the People’s Republic of Tannu Tuva, and read their initials across the page.
In March I took on the role of constructing an example puzzle with Rob’s idea.
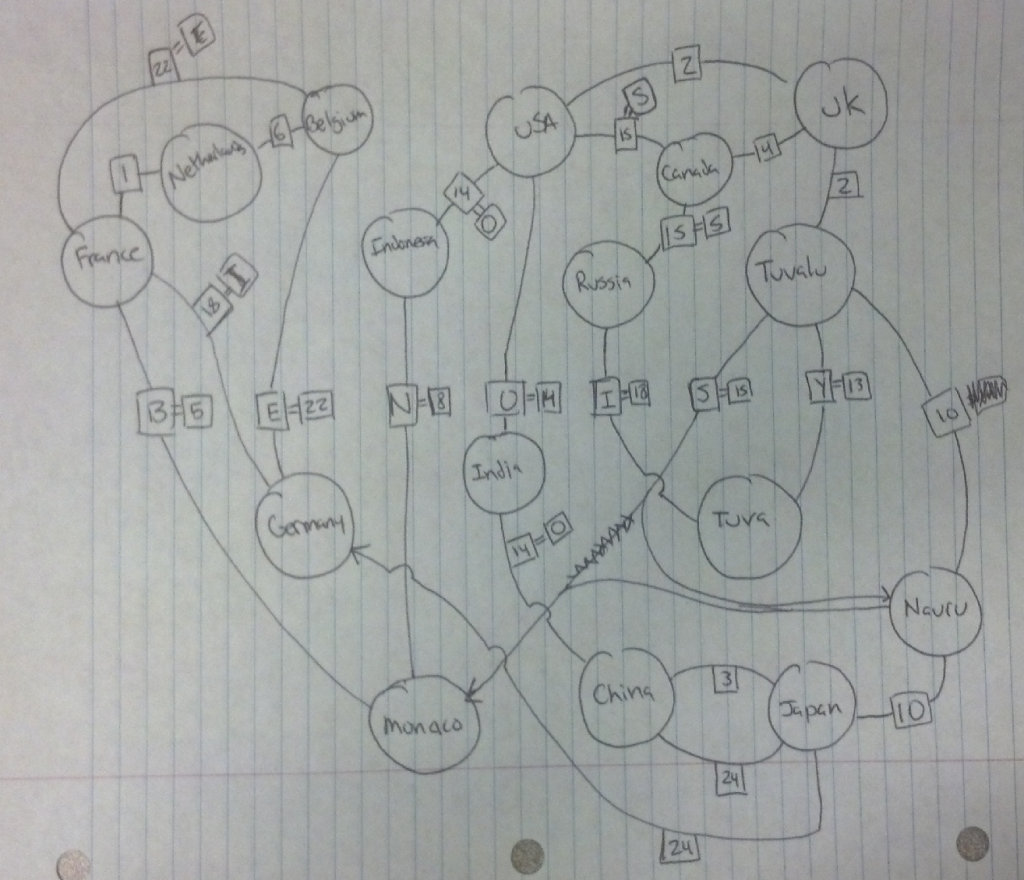
I never quite understood the “figure out the set of starting points (leaf nodes) that get you to the People’s Republic of Tannu Tuva, and read their initials across the page” part of Rob’s idea. I figured that if there a leaf nodes that don’t get you to Tuva, then it will be obvious which ones those are because they will be disjoint. That might even make them impossible to solve. So my constructions abandoned the concept of a tree all together and just use a graph. Pictured is my first attempt; The rules are specified by number in this google doc. I used numbers because they can be arbitrarily assigned to letters in order to spell nice words. One thing to notice is that this puzzle does not have an extraction mechanism, it doesn’t have an answer.
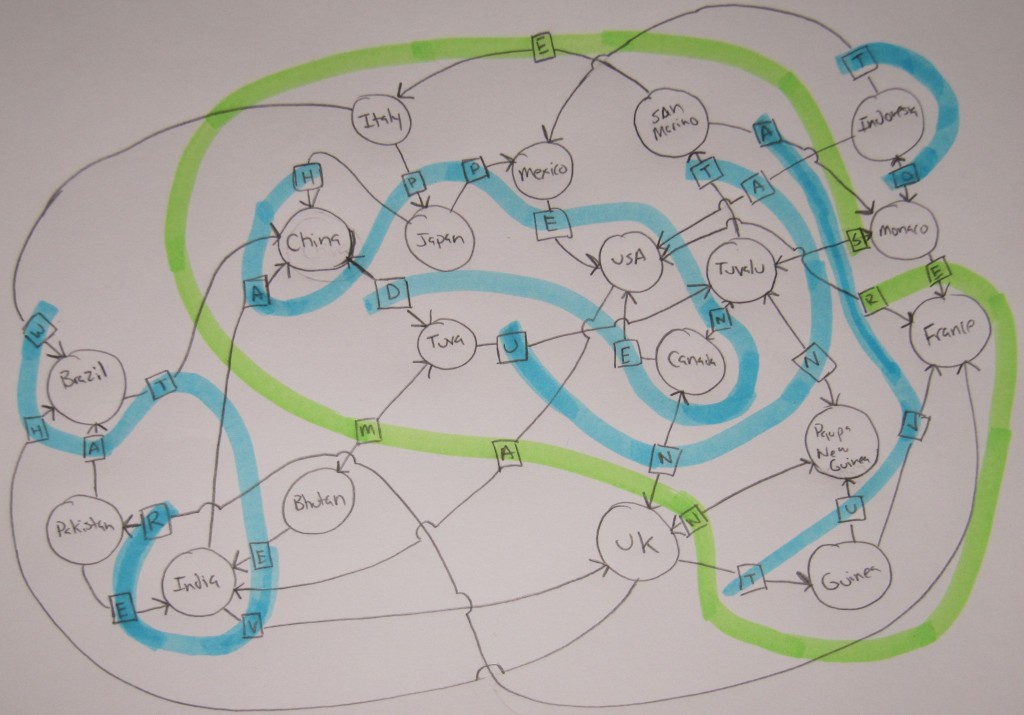
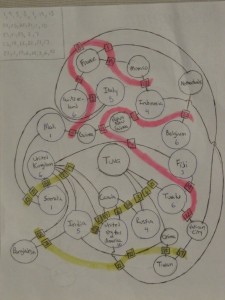The next draft actually has an extraction mechanism. If the circle has a number you take the Nth letter of the country, where N is that number. It forms a circle, but you can figure out where it starts. This draft should resolve to YOU JUST ASK ME, which is play on “You Just Ask Them,” a chapter from Surely You’re Joking, Mr. Feynman!. I think there is an error in it though. The key innovation in this version, other than an extraction mechanism is the colored ribbons which allow more flexibility in the graph layout while still spelling words with the relations. This allows a more complicated graph. In this case the two colors don’t mean anything, but the idea of having multiple colors will become important.
Shortly after I presented this work, the team moved away from the idea of having shell-metas in this round because the idea for the super-meta for the round was taking shape and it didn’t need shell-metas to work. So, I took this puzzle idea, and with, my editor Darby’s help we managed to covert this idea from a shell-meta, which takes input answers, to a regular puzzle, which does not. My first idea for this was to add a step to the start of the puzzle, which would basically provide the input answers, something like a word search or cryptic clues.
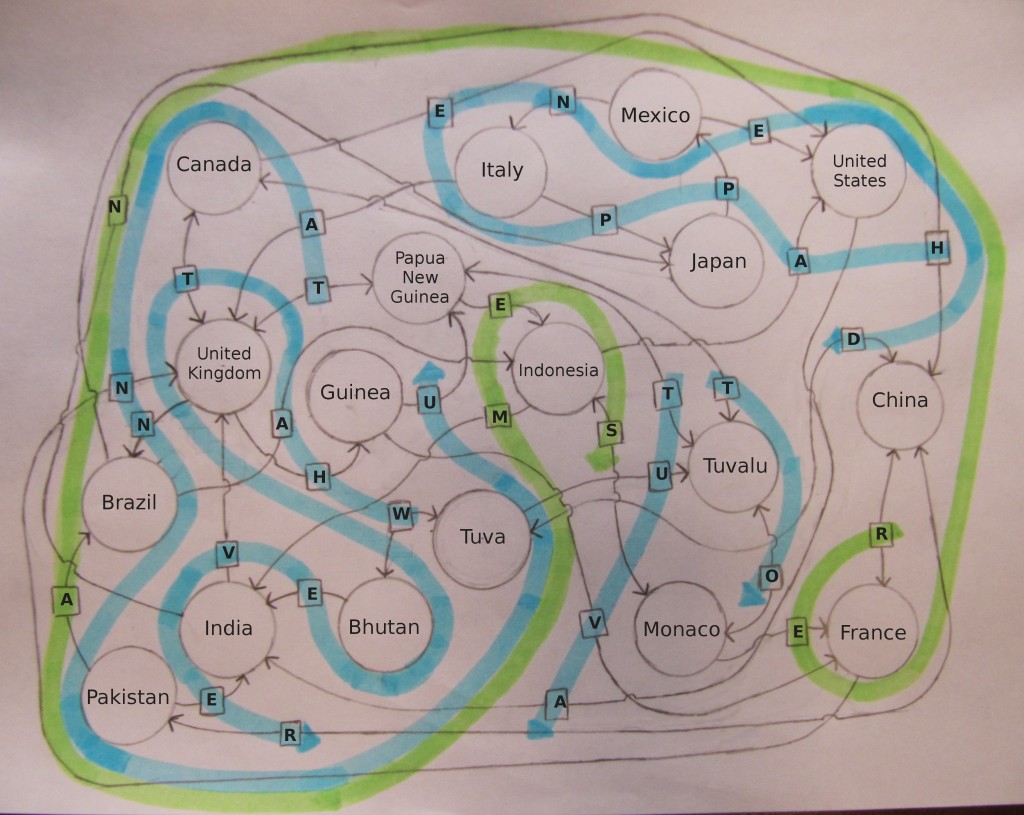
There were two key innovations that made this puzzle what it became. The first one is that Darby had the idea that we could eliminate the clunky extraction (of indexing in some circles) if the answer (or a clue phrase for the answer) were spelled out in a ribbon. The second one is that we should provide the alphabet mapping instead of solving for that while solving the logic puzzle. We didn’t know this yet, but the puzzle here doesn’t have very many constraints, which makes it quite hard to solve. The added constraint of having to find the alphabet mapping was just too much. I constructed a version that solved to BENOISY where the other letters that were not in a line had no meaning or pattern, seen below.
We didn’t really like the way this reduced the size of the graph, and we thought that the random letters would be too hard to figure out. After this version we brought back the ribbon concept. We decided to go with spelling out the actual answer RENAMES in a green ribbon and then spelling “Whatever Happened to Tannu Tuva,” the most famous Feynman quote about Tuva with the rest of the relationships in blue ribbons. This added a constraint in that once you figured out the quote you’d really only have to solve half of the logic puzzle. We thought about various methods for cluing the quote. At first we didn’t clue it at all. This version (below) goes with this set of instructions.
This version was put into test solving. Our solver, Adam, did a lot of work to come up with some good lists of countries for each rule, but we learned some of the lists we had been using were not as canonical as we though. He didn’t seem interested in solving the logic puzzle though.
What would it take to throw all the possible answers into a program to search for the answer? A lot of programming time, and unless the possibilities get cut down really quickly, the run time’ll be too high.
Back-of-the-envelope calculation: 200 countries in the world, so 40000 pairs. About 1000 pairs allowed by each unlabeled two-way arrow, so each two-way arrow restricts by a factor of 1/40. One-way arrows are phrased to assign a unique partner to each country, and there are 5 unrestricted ones of them, so also about a factor of 1/40. So the amount of constrainedness is about (1/40)^{27} and the number of possible assignments of countries is (200}^{26}, so with high probability either I’m missing some constraint or the arrows are arranged really, really carefully so this configuration is uniquely solvable. There are only about two triangles, which the same back-of-the-envelope calculations indicate should be way underconstrained, and one four-cycle containing Tuva.
Most of the constraints really do seem to be one-way arrows. I really don’t feel like wading through all the ambiguities in A, H, and W:
A, H, and W are orderings of countries by things with large measurement error and very small differences between the bottom countries. Different measures or people with very slightly different criteria and get slightly different results and quite different orders, and slight changes by the time hunt starts are likely to permute the order again. (And they do get different orders: the first three google results for “list of countries by population” for A have different results
Truth be told we had never proven the graph was uniquely solvable. We had not proven that you couldn’t fill in a different set of countries in a way that followed the directedness of the arrows. Proving that seemed really hard, but we were pretty confidant that the relationships out from Tuva were severely restricted and that from there it would be really difficult to go astray. We would not have been surprised if the whole graph could be solved in multiple ways, but we were pretty sure if the center circle had to be Tuva then it was unique, if you used the right lists.
One thing I learned from this report that I didn’t realize at first that the directedness of the arrows was a huge constraint. Having two kinds of arrows partitioned the rules set and reduced the complexity. When I decided we needed to have two kinds of arrows, that decision was made on a different basis. It was made on the basis that there were interesting rules for each type of arrow and not enough rules of any one arrow type to cover the alphabet. I could have left the directedness of the arrows ambiguous, but that seemed hard and evil on the face of it. So I didn’t want to do that. But What I hadn’t realized is how much power giving away direction gave the solvers. It turns out the power was used for good by making the puzzle easier to construct and easier to solve.
My number one rule when constructing was that I could only use an arrow between two countries if it was the only arrow of that directedness that could be drawn between those two countries. That is, the rule used must be unique in order to to specify a unique letter, which is a property we certainly wanted. For example I couldn’t draw a directed arrow from USA to Canada because that could be filled by either the “Longest Border With” rule or the “Immediately Larger in Total Land Area” rule. However, I could (and did) draw the reverse arrow because from Canada to USA also satisfies the “Longest Border With” rule, but it is the wrong direction for the land area rule. Similarly you can’t draw a bidirectional arrow between Tuvalu and United Kingdom because it could be either “Shares the Same Head of State” or “Both have a Cristian Official State Religion.” That is why there is a 4 cycle with the “Same Head of State” rule. Another area of constraint when constructing was ambiguity. It is unclear if the UK has an Cristian official state religion or not, for instance. England does, but the rest of the UK does not. So there is an ambiguous edge, an edge that I can not use, but it still causes me to not be able to use any other rule which would draw an edge that could be confused with it. It turns out that my construction spreadsheet was not capable of representing these rules and therefore always had to be tweaked by hand.
The results from this solve were many. The large changes were:
- We fixed a bunch of rules, and decided to use the CIA World Factbook as our canonical source whenever one was needed
- I actually had to come up with a whole new layout and letter assignment due to the changes incurred from using a different cannonical source. This took a huge amount of time and I even learned to use R to optimize graph layouts. However the graph for this puzzle is quite far from being one dimensional.
- We included “Whatever happened to Tannu Tuva?” as flavor text
- We fixed the wording on lots of rules to change tenses and provide or remove clarifying adjectives
This time there was a long wait for someone to fact check the puzzle. They came up with a number of issues, which required that I find hard eveidence to support the claims I was making. For example:
“The constitution provides for freedom of religion, and other laws and policies contributed to the generally free practice of religion. Although the Church of Tuvalu is by law the state church, this status has few ramifications other than to afford it “the privilege of performing special services on major national events.” The constitution provides for separation of church and state.”
The checker also found that Japan and India hand swapped positions on the GDP list and the arrow for them needed to be reversed. I managed to do this in a photo editor instead of redrawing the solution. After this check we arrived at what would be the final solution.
In this round of testsolving, tons of people looked at the puzzle. They came up with really great lists of countries for each rule, but no one could fill in the graph. In this version we gave away the text for the blue arrows as the flavor text of the puzzle. No research was required. All you had to do, the ahha was that the given quote fits in the boxes. You can figure this out right off the bat from a directedness and length argument. Eventually our best logic puzzler, Derek, figured this out. In his report he said:
It works, and it’ll keep a team busy, but I guess I ended up disappointed after spending a few hours thinking the puzzle was something different (ie, a logic puzzle) than it was. The “aha!” was more annoying than exciting. Many of the rules weren’t used, and the answer didn’t make much sense in context. Oh well.
We didn’t like the sound of that. We wanted a puzzle that was lots more fun than that. We wanted the logic puzzle that he also had wanted. We made two changes to make this happen. First we removed the quote from the flavor text and added a hint at the Tuva quote saying, “Feynman said it best.” Second, we added a list of countries which were the only ones that could appear in the puzzle. This made things much more constrained. You could still find the quote and make the directedness and length argument to start with, but it wasn’t the only ahha, you could also just do the logic puzzle. We test solved this, but we allowed solvers to use the previously compiled lists. They were able to easily pair down those lists based on the countries they were now allowed to use. This cleared up a lot of confusion. For instance, Bhutan is not the most obvious Buddhist country, that distiction falls to Cambodia. However, Cambodia is a dead end with the rules we have. You can get the Thailand from it, but from there you can’t get to anywhere great. Since Cambodia was not on the allowed list, finally no one was making that mistake anymore. I didn’t find this out until discussing the puzzle with solvers after the hunt, but this also reduced the work load to find the data. Since you could look up each country and then check off the rules that it could or couldn’t be used with.
As a side note, Cambodia and Bhutan were both in the running to become a member of the UN security council effective in time for me to use that fact in the puzzle. Sadly they were both up against South Korea, and South Korea won the seat. I had to wait for this election to be over in mid October before I could construct the final version. For a week or so I was UNSC elections junkie, but I couldn’t tell anyone about it.
South Korea did end up appearing in the list of allowed countries, but not because of its UNSC seat. I came up with the list of allowed countries by making sure that you could use every rule at least once. I tried to choose countries which satisfied more than one rule with other countries on the list. For instance Iran and North Korea had to make the list because they are the two unambiguous “Axis of Evil” countries left, since Iraq might not be considered the same country that was in the Axis anymore since it has a new regime. Then South Korea must appear because of the “DMZ” rule. The one rule which doesn’t have any countries to satisfy it is the “Not Full Member of the UN” rule for letter K. This rule is so tricky, because most nations that aren’t full members are not considered sovereign by at least one nation, for example Taiwan. The only country which everyone recognizes as sovereign that’s not a full member is the Vatican. Randall Munroe, commented to me at an event after the hunt, that he couldn’t find any of the listed countries that fit this rule. I told him that it was by design because the rule is so unwieldly. The truth is the rule is much eaiser when you get to define the list of countries, but since we added that so late in the process, I just ignored it. Plus, it is nice if you figure out it can’t be used, then you can pretend its not there, which makes the puzzle a little easier.
After most of the other puzzles in the hunt had been solved, testers finally came back and proved that the new version, with the list, was solvable, and more fun that the previous one. The solvers’ only comment was that we should replace the hand drawn picture. Mike Yi was able to turn my hand drawn version into the one you see in the puzzle. It is mostly exactly the same, but he did reroute some lines which improved the look. Overall I was proud how this puzzle turned out. Randall called it one of his favorites, which made me quite satisfied of a job well done. I think the development of this puzzle is a good lesson in how a puzzle that started off way too hard can made much easier while also being made much more fun. It did take 3 test solving iterations to do that, which was a lot of effort by many people on the team. We only had time for that because this idea was first drafted in March. If more of our puzzles had the time to iterate like this, I think we’d have had a much shorter, easier, and more fun hunt.